Guide to Constraint Programming

© Roman Barták, 1998

Contents

Prev
Up

Next

Constraint Satisfaction

Benchmarking and Algorithm Analysis

[academic bench] [industry bench] [random CSPs]

The computer science community has always been interested in "benchmarks" - standard problems by which performance and progress can be measured. One can distinguish two different categories of benchmarks:

  1. academic benchmarks
    These are artificial benchmarks developed by scientists at academic institutions to test research ideas. These benchmarks do not reflect necessarily the manufacturing reality.
  2. industry benchmarks
    These real-life benchmarks are based on real data sets obtained from the industry. The problem is how to obtain real data sets that are usually part of trade secret.

At this page I present two representative benchmark sets of both categories and I also give a brief description of Random CSPs which are used to identify extremely hard problems.

Academic (Artificial) Benchmarks

These academic benchmarks (sketch) are based on Brian Mayoh's family of benchmarks (1993). Although the benchmarks reflect a wide range of constraint programming applications, they form a family because their underlying constraint networks are variants of the 182 vertex graph G (one can get mini benchmark problems by using 79 vertex subgraph of the graph G).

Graph (selected part)

Graph description:
Vertex

Adjacent vertices

adr

tri ven apu mon alb

aeg

gre bul con smy eme

afg

ira tur kas del

alb

mon ser gre mon gre ion

alg

mor tun sah wme tun

...

...

Original map:

Problem Series

  1. DNA Sequencing
    vertices correspond to DNA fragments (adr: GACGGAGTTGGACGGTA ...); find most likely DNA string
  2. Coloring
    find four-coloring of the graph
  3. Layout
    vertex represents rectangular window; find windows configuration on the computer screen
  4. Scheduling
    vertices represent sessions, the adjacent sessions must not be scheduled at the same time; find the shortest schedule
  5. Control
    k-queen (at vertex) control all vertices within the distance k;
    • how few k-queens can be placed on G so all vertices are controlled
    • how many independent k-queens can be placed on G
  6. Colonization
    vertices represent regions in the world; play the game colonization
  7. Warehouse
    vertices represent regions in the world; find the best location of the manufacturers warehouses
  8. Spatio-temporal relations
    the vertices represent regions in 2D space, for each vertex, the relative position to all other vertices is given; find the feasible solution, i.e., placing for the 182 regions
  9. Diplomacy
    play the game Diplomacy (actually, the graph G comes from the Youngstown variant of Diplomacy)

Industry (Real-Life) Benchmarks

This is an example of planning and scheduling benchmark set (1995) which consist of a data set derived from real-life data and associated series of problems. It is based upon large scale assembly but it is applicable to a wide variety of problems in engineering, construction, and manufacturing that can generally be described as resource constrained project scheduling.

Data Set

Schedulable activities (575 activities, two 7,5 hour daily shifts)
Name (assemly.step)
Duration (H:M)
Labor (Px,Py,Pz,Pw)
Zone (Za,...,Zm)
...
...
...
...

Precedence relationship (between activities)
Predecessor
Successor
...
...

Activity plan (for rescheduling)
Activity name
Start time (Day/Shift+H:M)
...
...

Zone occupancy limits
Zone
Za
Zb
Zc
Zd
Ze
Zf
Zg
Zh
Zi
Zj
Zk
Zl
Zm
Max. occupancy
2
1
1
2
1
2
1
2
5
2
1
4
3

Labor limits
Labor pool
Px
Py
Pz
Pw
Shift 1
2
3
2
3
Shift 2
1
1
2
2

 

Problem Series

There are two problem series associated with the above data set. Problems 1 through 4 are concerned with schedule generation from scratch, while problems 5 through 11 are all concerned with schedule update and revision (rescheduling). The goal of most problems is to find minimum cycle time for the completion of the assembly.

  1. Precedence Scheduling
    ignore all labor and zone constraints, but respect all precedence constraints
  2. Resource Constrained Scheduling
    ignore all labor constraints, but respect all precedence and zone constraints
  3. Resource Constraint Scheduling, Non-Interruptible
    respect all precedence, zone and labor constraints, guarantee that each activity finishes within the same shift as started
  4. Resource Constraint Scheduling, Interruptible
    respect all precedence, zone and labor constraints, the activity can be finished in the next shift
  5. Insertion of New Work
    add new activities to the current schedule without rescheduling the current activities, start new activities as soon as possible
  6. Insertion of New Work with Delayed Start
    add new activities to the current schedule without rescheduling the current activities, start new activities as late as possible
  7. Daily Updates
    reschedule all work after the first day respecting completed work, work in progress, planned and delayed starts
  8. Daily Updates with a One-Week Horizon
    repeat the previous problem but restrict the schedule revisions to the first work week
  9. Temporary Perturbation of Labor Availability
    amend the schedule under the assumption that some of the labor will be assigned to a special project during the second, third and fourth work weeks
  10. Temporary Perturbation of Labor Availability with 4 Week Horizon
    repeat the previous problem but restrict the schedule revisions to only the second through fifth weeks
  11. Introduction of the Next Assembly
    start production of a second assembly on day 16 shift one, any of the work remaining on the first assembly be rescheduled, but do not perturb schedule prior to day 16
  12. Multiflow Production
    make eight copies of the activity data and schedule the start of a new assembly every 15 working days

For detail description of the above benchmark set visit the web site at http://www.neosoft.com/~benchmrx.

Random CSPs

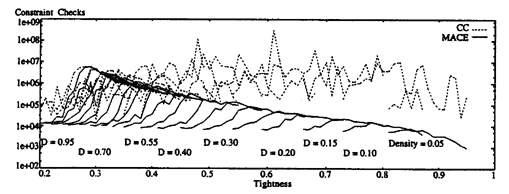
The benchmark sets are used to test algorithms for particular problems, but in recent years, there has been a growing interest in the study of the relation between the parameters that define an instance of CSP in general (i.e., the number of variables, domain size, tightness and density of constraints). Therefore the notion of randomly generated binary CSPs was introduced to describe the classes of CSPs. These classes are then studied using empirical methods.

Each set of random constraint satisfaction problems is defined by the 4-tuple <n,m,p1,p2>, where:

  • n is the number of variables,
  • m is the number of values in each variable's domain,
  • p1 is the proportion of pairs of variables which have a constraint between them, i.e., the constraint density (there are p1 * n * (n-1)/2 constraints/edges in the graph)
  • p2 is the proportion of pairs of values which are inconsistent for a pair of variables if there is a constraint between them, i.e., the constraint tightness (there are p2 * m2 incompatible pairs of values in each constraint).

The problem generator ensures that all problems are generated with connected constraint graphs, so that the resultant problem cannot be decomposed into smaller components: disconnected graphs are simply discarded and new graphs are generated until a connected one is found.

When discussing problem size, the researches are usually referring to the tuple <n,m>. Phase transitions from under- to over-constrained problems are observed as p2 varies, while n, m and p1 are kept fixed; classes of randomly-generated problems with fixed n, m and p1 and varying p2 are referred to by tuple <n,m,p1>.


Comparison of algorithms using random CSPs

 

[academic bench] [industry bench] [random CSPs]

Contents

Prev
Up

Next
Designed and maintained by Roman Barták