Nombril korespondenčně.
chessandgo (čtyřnásobný mistr světa) - hráno na mistrovství světa.
chessandgo/hanzack finálová hra mistrovství 2012
chessandgo začátky
V době, kdy počítačový program DeepBlue porazil šachového mistra světa Gari Kasparova, se Omar Sayed rozhodl vymyslet hru, kde budou lidi úspěšnější než počítače. Rozhodl se zachovat prostředky, které měly šachy. Vznikla tak hra, kterou je možno hrát s šachovými figurkami na šachovnici. Vše naznačuje tomu, že se mu podařilo vyladit pravidla dobře. Hra má velice jednoduchá pravidla a přitom je strategicky i takticky velice bohatá.
Omar koncem roku 2002 vsadil 10 000 $ do roku 2020 jako výzvu pro počítačový program, který na běžném HW dokáže porazit nejlepší lidské hráče. Na kratší dobu přidávají v šanc své peníze i další lidé. Například loni vsadil 1 000 $ do roku 2020 i Leo Broukhis (který vypsal v roce 1996 výzvu datové komprese).
Kromě toho, že Omar hru vymyslel, vytvořil i internetové rozhraní umožňující hru lidem navzájem z celého světa či proti botům na serveru rozličné úrovně a herního stylu. Celé herní prostředí je bezplatné, turnaje jsou doprovázeny internetovým rozhlasovým vysíláním a všechny partie jsou archivovány a kdokoli si je může kdykoli přehrát. Nejdůležitější partie (mistrovství světa) jsou i s komentáři připraveny ke stažení ve formě .avi videí. Vyšly dvě knihy týkající se Arimaa. Jednu vydal dvojnásobný mistr světa Karl Junke (Fritzlein), druhou nyní čtyřnásobný mistr světa Jean Daligault (chessandgo).
Ke hře potřebujeme tak jako pro šachy čtvercovou desku 8×8 sady 16 figurek ve dvou barvách, kde figurky jsou od nejsilnějších po nejslabší v následujících počtech 1, 1, 2, 2, 2, 8. Na rozdíl od šachů jsou figurky pojmenovány po zvířatech slon, velbloud, kůň, pes, kočka a králík, ale šachisti klidně mohou použít král, dáma, věž, střelec, jezdec, pěšec (pro začínající šachysty je výhodnější pořadí podle velikosti figurek král, dáma, střelec, věž, jezdec, pěšec).
Hra začíná na prázdné desce, začínající hráč (bílý resp. zlatý) rozestaví svých 16 figurek na první dvě řady desky. Poté druhý hráč (černý resp. stříbrný) rezestaví svých 16 figurek na sedmou a osmou řadu desky (nejbližší 2 řady k hráči). Na rozdíl od šachů, kde je rozestavění jediné a nepočítá se za první tah, připadá zde do úvahy 16!/(1!1!2!2!2!8!)=64 864 800 pro každého hráče.
Pole C3, C6, F3, F6 dle šachové notace jsou pasti.
Figurka, která nesousedí (přes hranu) s figurkou stejného hráče je v pravidlech penalizována (viz níže).
Pravidla pro pohyby figurek jsou v Arimma velice jednoduchá. Figurkou můžeme pohnout na (přes hranu) sousedící prázdné políčko.
Složitost do hry přináší fakt, že hráč ve svém tahu pohne až 4krát, pro jednotlivé pohyby může použít různé figurky. Hýbat nemusí jen svojí figurkou, může pohnout i soupeřovou. V takovém případě se jedná o dvojici nerozlučných pohybů, dvou sousedících figurek, kdy hráčova figurka je silnější. Soupeřova figurka může být tažena (hráč přesune nejprve svojí figurku a na uvolněné pole přitáhne soupeřovu) nebo tlačena (hráčova figurka obsadí pole uvolněné soupeřovou figurkou). Pohyb hráčovy figurky může být součástí jen jedné dojice nerozlučných pohybů, trojice pohybů, kde hráčova figurka současně tlačí i táhne není přípustná.
Cílem hráčů je dostat svého králíka na protější konec desky (gól). Alternativním cílem je sebrat soupeři všechny králíky. Hráč prohrává taky v případě, kdy nemůže zahrát.
Počítače hrají hry bez porozumění pozice, využívají své rychlosti a porozumění nahrazují
intenzivním prohledáváním možností.

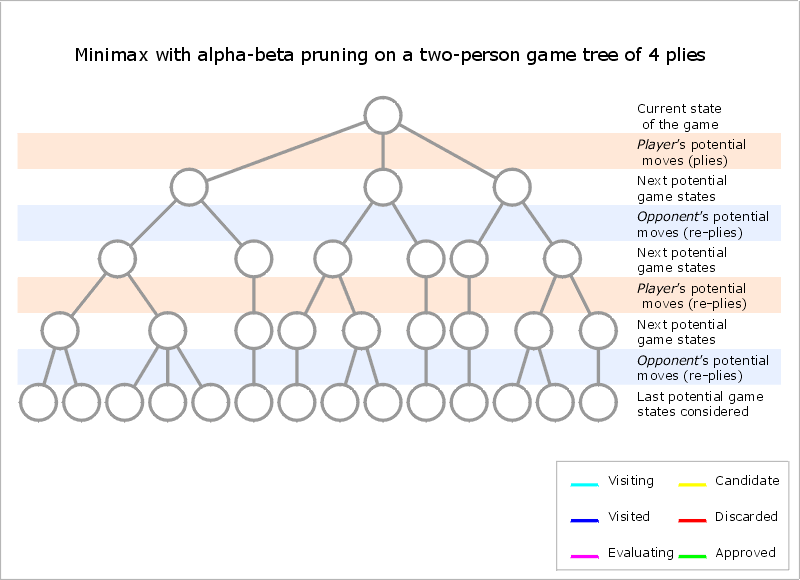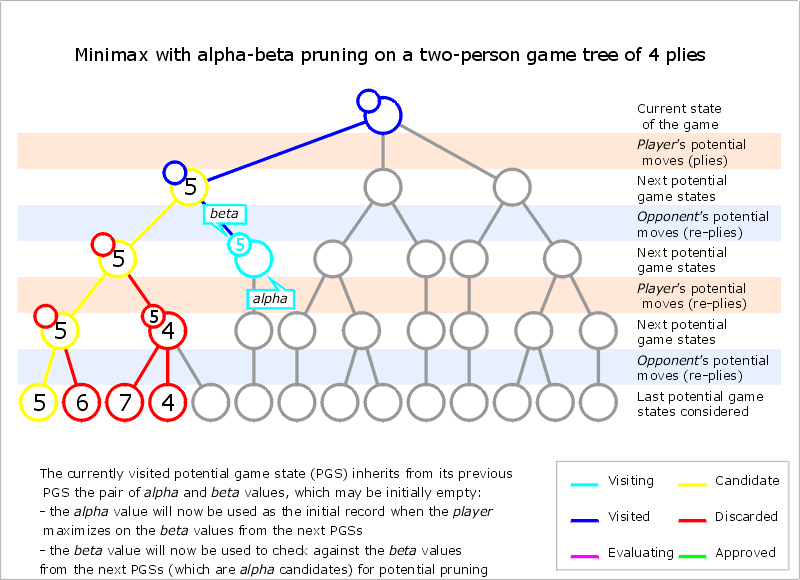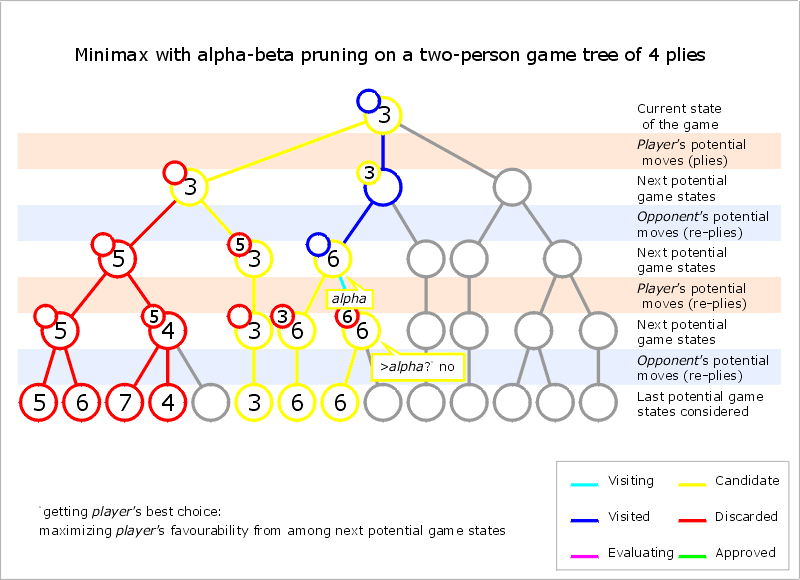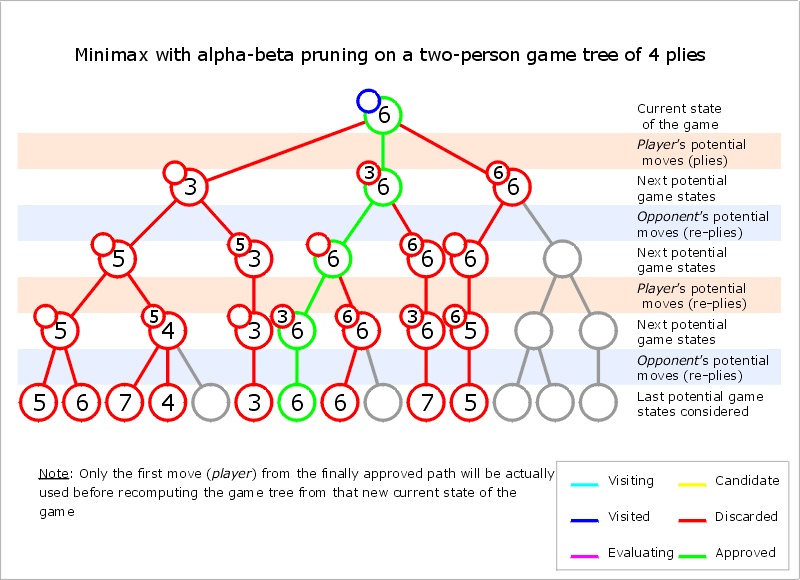
Základním algoritmem je minimax s alfa/beta prořezáváním. Algoritmus je založen na ohodnocovací funkci, vyjadřující pravděpodobný výsledek hry. V koncových pozicích se pravděpodobnost mění v jistotu.
Program určí hloubku prohledávání a snaží se vždy pro hráče na tahu maximalizovat pravděpodobnost jeho výhry počítanou v dané hloubce. Z hlediska jednoho hráče jde o maximalizaci v jeho tazích a minimalizaci v tazích soupeře.
Pokud program v dané hloubce ukončí prohledávání a zbývá dost času, může zvětšit hloubku a postup opakovat. Opakování samozřejmě není potřeba, je-li výsledek znám s jistotou.
Když dojde čas vyhrazený na prohledávání, program vrátí tah, pro nějž vychází pravděpodobnost výhry nejvyšší (v závislosti na implementaci buď z poslední zcela prohledané hloubky nebo z hloubky aktuálně prohledávané).
Alfa/beta prořezávání zabraňuje prohledávání podstromů, pokud již víme, že nemají vliv na výběr nejlepšího tahu. Například, pokud dosud nejlepší tah má pravděpodobnost výhry 1/2 a pro náš testovaný tah nalezneme soupeřův tah, po němž je pravděpodobnost naší výhry jen 1/4, nemá smysl zkoušet další tahy soupeře, protože již máme dostatečný důvod testovaný tah nehrát. Alfa, beta jsou dolní a horní odhady optimální dosažitelné pravděpodobnosti používané k prořezávání.
Alfa beta prořezávání je tím lepší, čím dříve narazíme na nejlepší tah. Při optimálním řazení tahů dosahuje alfa/beta strom téměř stejné velikosti jako minimax strom poloviční hloubky.
Algoritmy používají další významné triky zvyšující efektivitu prohledávání.
Jedním z nich jsou takzvané transpoziční tabulky, kde si pamatujeme výsledky prohledávání a pokud narazíme na pozici, kterou jsme již prohledávali, můžeme využít výsledků prohledávání.
Transpoziční tabulky ušetří prohledávání, pokud stejnou pozici dostaneme jiným pořadím tahů. Ukládání nejlepšího protitahu v transpozičních tabulkách vylepšuje řazení tahů při opakování prohladávání pro větší hloubku.
Další technikou je pamatovat si výjimečně úspěšné tahy (způsobující oříznutí stromu) a předřazovat tyto tahy,
jsou-li legální, před ostatní tahy (je velká šance, že tentýž tah způsobí oříznutí i v jiných větvích výpočtu
a čím dříve se nám podaří oříznout, tím lépe).
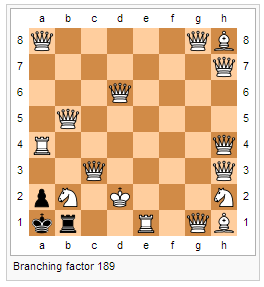

Metoda je velice úspěšná pro šachy. Základem úspěchu je existence kvalitní ohodnocovací funkce pro šachy a schopnost programů prohledávat s ní do dostatečně velké hloubky. To je umožněno tím, že pro hráče na tahu připadá v běžné pozici 35 až 38 možných tahů. Maximální větvení v šachu nejspíš nepřesahuje 200. Bohužel v Arimaa připadá na hráče v běžné pozici kolem 10 000 možných tahů a maximální větvení přesahuje 338 000.
Při použití stejných technik prohledávání je proto program pro hru Arimaa schopen prohledávat do zhruba 2.5 krát menší hloubky. Horší je to ale s ohodnocovací funkcí, kde u šachů je materiální převaha mnohem podstatnější faktor a v případě ostrých pozic (možnost braní, matové hrozby, hrozby proměn) není až tak náročné přidat prohledání do tiché pozice. V Arimaa je takové prohledání do tiché pozice většinou samo o sobě mimo výpočetní možnosti stroje.
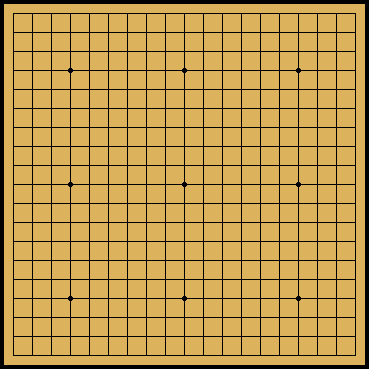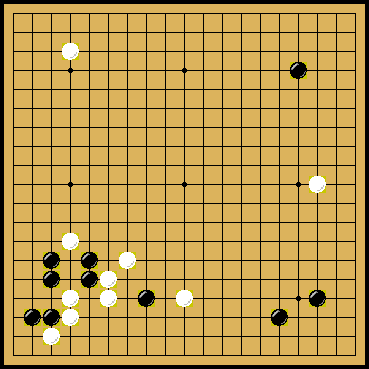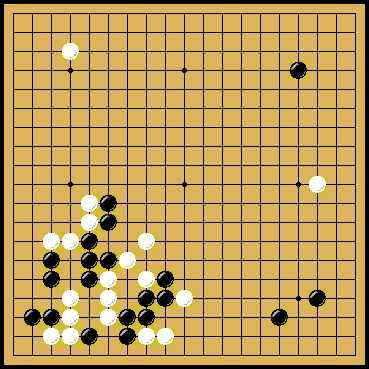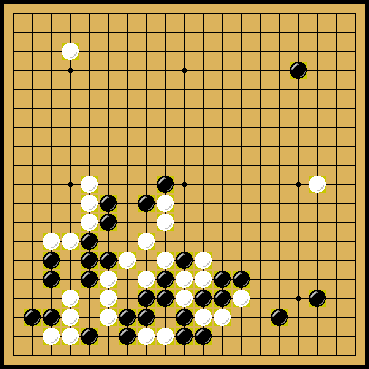
Pro hru go jsou úspěšnější programy pracující na jiném principu. Důvodů je několik. Jedním z nich je neexistence efektivní ohodnocovací funkce, druhým je veliká hloubka partie. Maximální větvící faktor 192=381 u go připadá na prázdnou desku, s postupujícím zaplněním desky klesá. Bodově nejdůležitější je počáteční boj o vliv, který se odehrává řekněme 100 půltahů před koncem sehrávky. Taktické vyhodnocení takovýchto tahů je zcela mimo možnosti minimax prohledávání.
Prosadila se metoda založená na statistikách náhodného vzorkování nazvaná Monte-Carlo tree search. Principem je ohodnocení pozice na základě náhodné sehrávky. Tah, který bude pro hráče zkoumán je vybrán s ohledem na předchozí statistiku (očekávanou pravděpodobnost úspěchu) tohoto tahu, ale i s ohledem na četnost, kolikrát byl tah zkoumán (pravděpodobnost výběru je součtem pravděpodobnosti úspěchu a bonifikace za nedostatečné prohledání (wi/ni+c√(log n/ni))). Ve chvíli, kdy počet ni, kolikrát byl tah prohledán překročí stanovený práh, stává se tah vnitřním vrcholem stromu a pokud je vybrán jako tah, není pro něj spouštěna náhodná sehrávka, ale je pro něj vybírán následník dle stejného principu (volba tahu preferuje vítězství vždy z pohledu hráče na tahu).
Po vypršení času určeného k prohledávání je zahrán nejčastěji prohledávaný tah.
Výhodou hry go je, že dobrý průsečík (tah), je dobrý pro oba hráče, navíc, pokud nedojde ke změně v lokálním okolí, zůstává dobrým i nadále. To vedlo k zavedení statistiky pro průsečíky, sdílené pro všechny simulace. Ve výběru tahu je navíc zvažována i tato statistika průsečíků, nicméně význam této statistiky s rostoucím počtem n prohledávání tahu klesá. Význam této sdílené statistiky je v efektivním nasměrování počátečního růstu stromu a velmi významně se projevuje v herní síle programu.
Go je typickým příkladem, vhodnými hrami jsou obdobné hry boje o území jako Y (AZ kvíz), případně hry bez zatajení informace, ale s náhodou jako například METRO.
Bohužel v Arimaa se přípustné tahy v průběhu partie významně mění a ač je kvalifikovaná obrana srovnatelně úspěšná s kvalifikovaným útokem, náhodná obrana je mnohem slabší než náhodný útok.
Z toho nevyplývá, že by MCTS algoritmus nemohl být pro Arimaa úspěšný. Pouze to znamená, že náhodné sehrávky nemohou hrát všechny tahy se stejnou pravděpodobností. Bez nějaké ohodnocovací funkce, která by tahům přidělila váhy se tak asi neobejdeme.
Další potíž přináší rozhodnutí, jak náhodnou sehrávku ukončit. Je efektivní dohrávat až do konce partie, nebo jen určitý pevný počet tahů, zakončený ohodnocením pozice.
Další podstatnou komplikací je velikost MCTS stromu. Standardní MCTS ve chvíli kdy začíná prohledávání, případně když se vrchol stává vnitřním vrcholem MCTS stromu začne tím, že pro každý možný tah v pozici provede jednu simulaci. V případě obrovského větvícího faktoru hry Arimaa ja expanze vrcholu velice nákladná jak kvůli paměťové, tak kvůli časové náročnosti. Pravděpodobně by vrchol musel být expandován v několika úrovních expanze, každá úroveň by vyžadovala překročení svého vlastního prahu počtu simulací daného tahu. Opět by bylo potřeba vhodnou ohodnocovací funkci, která by vybírala tahy, které mají být expandovány na příslušných úrovních expanze.
Domnívám se, že i v MCTS se (v závislosti na implementačních rozhodnutích) vyskytuje problém horizontu, projevuje se tím, že po expanzi tahu do určité hloubky dochází k podstatnému zhoršení statistiky úspěšnosti tahu. Výsledkem je to, že MCTS strom expanduje mnohem víc do šířky než do hloubky.
Jednou z možností jak omezit velikost prohledávaného stromu je při vhodném řazení tahů část tahů v závislosti na aktuální hloubce prohledávání vůbec neprohledávat (do hloubky d je prohledávána pouze nejlepší část tahů dle ohodnocení v hloubce d-1). Očekávanou výhodou tohoto postupu je, že nadějné tahy budou prohledány do větší hloubky, čímž by mohl být potlačen efekt horizontu. Nevýhodou je, vysoká paměťová náročnost algoritmu, ale i závislost na kvalitní ohodnocovací funkci.
Pokud má prořezávání přinést oproti alfa/beta prořezávání (při očekávaném dobrém pořadí tahů) smysl, musí být prohledávána velmi malá část tahů.